関数の統一

今日：1 合計：950

前講座では関数の分割を扱いましたが，今回はその逆，関数の統一について扱いたいと思います．

よくある状況

まずは非常に良くある関数の統一について．これは他の講座にも書いてあるかと思いますが一応振れておきます．二倍関数と三倍関数を両方使いたい，と言うときに以下のように変数を増やす事で解決する事が多くあります．

次に以下の状況について考えましょう．

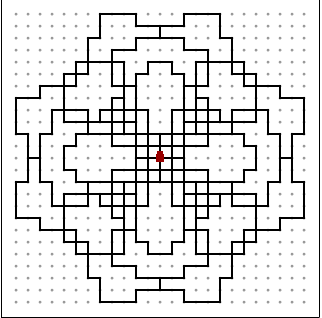
経路見えないよと言う人は以下の三つをご覧ください

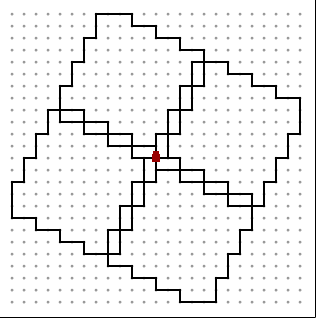
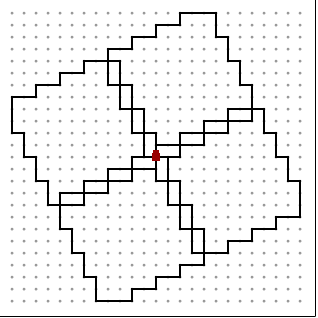
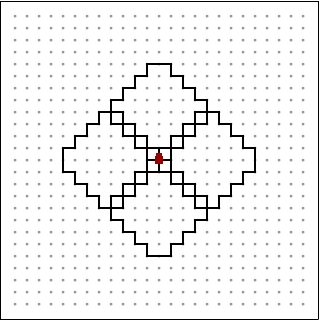
この三つを重ねたものになります． ssrsl,srssl,srslというパーツを四つくっつけて正方形にして四回繰り返す，と言うような事をすれば良いのでひとまず次を得ます

a(X):XXXX
a(a(a(ssrsl)r)r)a(a(a(srssl)r)r)a(a(a(srsl)r)r)
(35B)

ここでa()の後ろにrをつける事で短縮

a(X):XXXXr
a(a(a(ssrsl)))a(a(a(srssl)))a(a(a(srsl)))
(30B)

些細な短縮ですが，四倍を統一して

a(X):XXXXr
a(a(a(ssrsl))a(a(srssl))a(a(srsl)))
(28B)

ここで一変数に寄るパーツの圧縮を用いるとb(X):sXrslを用いる事で

a(X):XXXXr
b(X):sXrsl
a(a(a(sb()))a(a(b(s)))a(a(b())))
(26B)

しかしここでa(a(X))というaを二回施した関数が三回も使われている事に注目します．この関数をc(X)としたときにc(X)とb(X)を統一する事によって圧縮が効くのでやってみます

a(X):XXXXr
d(X,Y):a(a(sXrYsl))
a(d(s,)d(,s)d(,))
(24B)

（二変数にしたのはa(a(X))の中身に合わせるため）

このように見た目上はあたかも新しい関数を生み出していますが，裏では二つの関数を合成していると言う感じです．