![[PukiWiki]](image/hojwiki.png "[PukiWiki]")
まず，12B構文自体が初耳という方は有理数の成長速度2を参照してください．
本講座は，12B構文を使いこなす上でポイントとなりうる点を，執筆者のおさらいも兼ねて列挙してみるという目的で作成しました．
12B構文及びその変種についてはmasさんが書いた講座12B構文の周辺のほうに詳細が書かれており，今回触れる内容もこの記事と比較してめちゃくちゃ新しいと思える内容でもないかもしれません．
執筆者も当然使いこなせているわけではないので，他にポイントがあれば共有したいと思っております．
やや長くなったので目次を先に書いておきます．
�‘団蠅寮�長段階切り出し
��15B構文？
��クレイジー12B構文
�ね諭垢扮�用
��solver作成時の注意点および枝刈りポイント
こちらは12B構文の記事の「より複雑な構文」にて説明されている範囲のコードですが，少し意味づけができるので再度紹介します．
以下のコードを実行してみましょう．
a(X):a(X-1)sa(X-1)l a(9)
本コードは以下のコードにて実行されるXの10段階目を展開すると同一になります．
f(X):Xf(XsXl) f()
実際数値を用いて以下のように書くと同一の動きを書くことができます．
a(X):a(X-1)sa(X-1)l b(X):a(X)b(X+1) b(1)
例題: Problem 2001
続いて以下のコードを見てみましょう．
a(X):a(X-1)sa(X-2)l a(9)
このコードも実は以下の10段階目を切り抜いている，と説明できます．
f(X,Y):Xf(XsYl,X) f(,)
実際に以下を実行すると同一の動きが実現されていると確認できます．
a(X):a(X-1)sa(X-2)l b(X):a(X)b(X+1) b(1)
一般にa(X):ua(X-n)va(X-m)w という書き方では，u [n段階前のパーツ] v [m段階前のパーツ] w というような成長方法を実現しています．
(max(n,m)変数で実行部単一文字，初項はなし，というコードが対応物となります．）
基本的に既存の乱歩の成長段階ズラして組み合わせたものを実行しているので，綺麗な動きをする例は作れないという認識ですが，この手法で生成したランダムウォークでbest解になるのも多くあります．
検索している人が多くない印象なので，今15B以下のbest解でもこの方法で更新できるものはあると思います．
ちなみに小ネタになりますが，乱歩的な動きの方は実は https://www.cnblogs.com/duguguiyu/archive/2007/12/07/986017.html にて紹介されています．活用例は見当たりませんが実は既知テクだったんですね〜．
ただし後ろを+にして規則的動きを実現する，いわゆる「12B構文」の方は誰も活用できていなかったみたいですね．
このコラム（？）によると1424は本家マシンで実行3時間かかったとか，当時のガチ勢の中にも乱歩使う人と使わない人がいた話だとか（chokudaiさんは使わない側だったらしい？）今後の展望だとかが書かれています．
ガチ勢に知識の共有を求めている文章もあって，こういうのを見るとmasさんやsnukeさんの講座のありがたさを実感できます．
ここでは
a(X):[1]a(X-i)[2]a(X-j)[3]a(X+k) a(n)
という形の構文について触れます．i,j,k,nは正整数です．意味をなす最小のbyte数が15ということで15B構文としていますが全く名称は定まってないです．
構造としてはiで割った商の回数[1]を実行し，iで割ったあまりをjで割った商の回数[1][2]を実行した後[3]を実行し，jで割ったあまりにkを足す というのを繰り返すコードになっています．
構造上，以下の制約があります．
また，12B構文で実現可能な動きとの差別化を図る上で i は j よりもだいぶ大きい (具体的には i > 2j くらい？)としてもいいかもしれません．
最後の X+k が「 i で割った商がちょうど切り替わりそうな値」が入るように調整をすると，この構文に特有な動きが実現できます．
k として i * n - j + 1 ~ i * n - 1 あたりを採用すると特有の動きになりやすいです．また，最終的には j で割った余りがループに寄与するので， j が周期の基準となります．(周期の長さがjとは限りません．)
また，[1][2][3]全てに命令を入れれば基本的に特異な動きにはなります．
実際に以下の二つのコードを動かしてみましょう
a(X):sa(X-27)a(X-4)ra(X+52) a(29)
a(X):sa(X-27)a(X-4)ra(X+53) a(29)
一つ目は 2(初項) [7 3 7] [7 3 7]...という数列を実現します．
二つ目は 2(初項) [3 7 3] [3 7 3]...という数列を実現します．
12B構文と異なるのは，数列に現れる数の差をある程度大きくできるという点です．
次に，実際に数列を作成してみましょう．
実際に作成するとなると，出てくる数値の調整はともかく，周期の調整は手動で出すのはかなり難しいです．少なくとも私の認識ではある程度値を決めたら試し撃ち，ないしsolverを活用するという感じです．
問題1 5 9 2 9 9 2 9 9 2 9
問題2 2 7 6 3 7 6 3 7 6 3
答え1
a(X):sa(X-35)a(X-4)ra(X+33) a(142)
前の例と合わせて a b a a b a （a>b) というタイプの数列を作るには，
i = (a - 1) * 4 + 3 , j = 4, k = (a - 1) * 4 + 1 + (b - 2) * i
と置くとうまくいきます．a < b のケースも一般化してみてください~．
答え2
a(X):sa(X-27)a(X-5)ra(X+51) a(29)
こういう数列も実現可能です．
jをいじってどんな周期が実現できるか実験するのが良いと思います．
最後に，いくつか綺麗な模様を紹介して終わります．いろんなパターンがあると思われます．動き（≒構成可能な数列）をある程度把握した後はパーツを固定してsolverで検索するという感じになると思います．
まだまだ未知な部分も多いので調査して行って欲しい範囲です．
a(X):sa(X-43)rsla(X-17)ra(X+165) a(2)
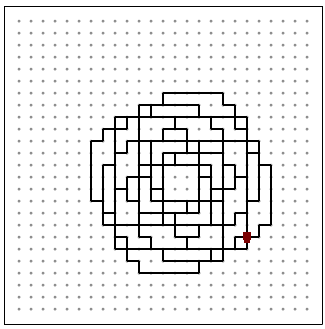
a(X):sa(X-144)sra(X-52)ssa(X+159) a(2)
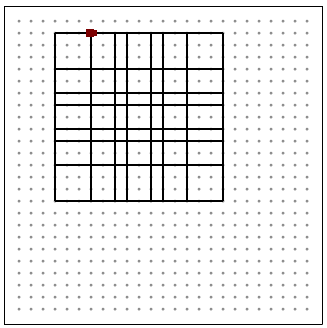
a(X):sa(X-43)rsra(X-17)ra(X+165) a(2)
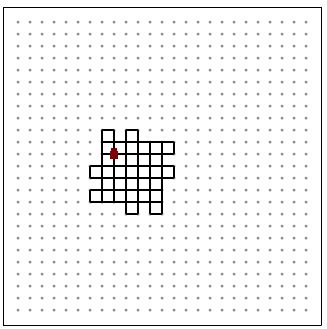
関連問題: Problem 1589 Problem 1955 Problem 1970
命名は_misakiさんの雑記から引用しています．
まずは12B構文を一般化して表記した以下の形を確認してみましょう．
a(T):[1]a(AT+B)[2]a(CT+D) a(E)
AT+Bの部分について，上記の構文が意味をなすものに絞ってみましょう．条件を整理すると以下の通りです．
・途中で255を超えない ・繰り返す途中で0以下になる
基本的なケースにおいては，上記条件をすべて満たし，意味づけも比較的容易な A=1, B<0 を前提としていましたが，実はこの部分はAとBの正負が異なり（AB<0)，Aが-1でないケースに対して有意なものが存在します．
Aの正負で少し状況が変わるので，それぞれ見ていきましょう．
Bは負なので，見易さのためにAT-B （B>0) と書き直すことにします．また，A=1は除外します．~
発散を防ぐために，代入後に値が小さくなる必要があることを考慮すると，AT-B < T ⇔ T < B/(A-1) が必要になります．（つまり，ある程度小さい値でループする必要があります）
この辺に注意をして，数値設定をする必要があります．
こちらも応用が効きそうなものや綺麗な模様がたくさんありますが，詳細は自分も深くは把握できていません．色々試してみると良いと思います．
いくつかの例を紹介しておきます．
a(X):sa(X+X-113)ra(X+13) a(11)
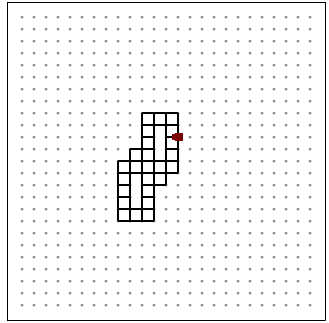
a(X):sa(X+X-177)ra(X+X) a(1)
a(X):sa(X+X-169)ra(169-X) a(1)
（見やすくするために最初ちょっと移動してます）
CT+Dの部分は大きすぎると桁溢れしてしまいます．CはA以下まで許容されると思われるため，二つ目のようなケースも考えられます．
また，Aが3以上になるとAT-Bが0以下になるスピードが一気に高まり，意味のある形を構成できなくなります．(この辺執筆者の調査及び理解が甘いです）
A=-1は二種類の値が交互に出てきてしまう形になるため，意味がないです．
Aが正の時と異なり，一項目で発散由来の条件に気をつける必要はないですが，ある程度大きな値が第二項に渡されるため，CT+Dとの兼ね合いには注意する必要があります．
いくつかの例を紹介します．
a(X):sa(219-X-X)ra(229-X) a(1)
a(X):sa(109-X-X)la(X-9) a(1)
どの形についても，周期的に繰り返される影響で見た目自体は綺麗ですが，繰り返す前のパーツ自体はランダムウォークと言ってもよいと思います．
また，この手法だと基本的な12B構文（後ろ側をいじるもの）よりも少ないbyte数で特定の数列を再現できたりします．
関連問題: Problem 2068, Problem 2071
2068はa(X):sa(X+X-n)la(X+X) a(m) のパターンです．大まかな形はnで決まるので，m=1で固定して，nを動かせば手でも解けると思います．
2070は実は盤面上の数字を使うと当てはまるものがあったりしますが，solver推奨と思います．
12B構文は非常に汎用性が高く，様々な応用があります．上で述べた数値関数をいじる応用も面白いですが，ここではそれ以外の応用を紹介します．
ひとまず三つ紹介します．
12B構文はパーツの長さの数列を制御するもの，という捉え方が多いかもしれませんが，パーツを固定して向きを制御するように使うこともできます．
r ないし l は4の倍数個並ぶと打ち消されるため，特定のパーツを並べるという際に向きの方の数列だと捉えることで問題が解けることもあります．
以下の例のようなパーツの並べ方を実現できます．
a(X):ra(X-56)ssa(X+17) a(2)
また，状況によっては同じ12B構文でもこちらの方法で縮むことがあります．以下を比較してみてください．
a(X):lsrsa(X-3)ra(X+7) a(2)
a(X):la(X-10)srsa(X+37) a(2)
上は15Bですが下は14Bになっています．上の向きの無駄を下で解消しているというイメージです．
パーツの両端のどちらかが向きの時はこの圧縮が使える可能性があります．
関連問題 Problem 1705
基本的な12B構文は特定のパーツを実行する回数の数列を制御するようなものでしたが，変数を増やすことで成長速度を制御することも可能です．
以下のコードを実行してみましょう．
a(X,Y):a(sX,Y-5)Xra(X,Y+3) a(,11)
成長過程の数列に対して適合する12B構文を見つけることでいろいろなことができるようになります．
関連問題
4-2のような成長速度を制御するタイプの類似物ですが，パーツを実行する回数の方を12B構文で制御するというパターンも存在します． 以下を見てみましょう．
a(X,Y):Xa(X,Y-5)a(ssX,Y+23) a(r,11)
渦の長さで言うと次のような数列を実現しています．
[0 0 0 2 2 2 2 2 4 4 4 4 4 4 5 5 5 5 5 ]
同じパーツごとに個数を書く形で整理すると以下の通りです．[0が3個] [2が5個] [4が6個] [6が5個] [8が6個]
このように成長させたパーツを何回実行するか，という部分を制御することでうまくかける問題もあります．
関連問題 Problem 0091Problem 0372など
平方数の時に成長をいじるタイプもこの手法で圧縮が効くケースが多いです.
4-2とほぼ同様ですが，少し応用的なコードを紹介します.
まず，有理数の成長にある以下のコードを思い出しましょう．
a(X):sa(X-37)ra(Y+83) a(1) ~
ロの字を書くコードになります．このロ字をパーツとしていろいろな箇所で使用したいとき，上記のコードでは無限ループになってしまう関係で使う場面がどうしても限られてしまいます．
そこで，以下のコードを実行してみてください．
a(X,Y):a(X-37,Ys)Ya(X+83,Yr) a(1,)
12B構文で生成しているパーツの途中経過を二変数目に保存してZ字を描く9B乱歩チックに配置しています．うまく数値や実行部分をいじることで応用が見込めると思います．
うまい活用方法は現在調査中です．
以上四つを紹介しました．当然数値の部分についてクレイジー12B構文や乱歩的構成を適用できる可能性もあります．
特に乱歩的構成（12B構文のB,Dがマイナスのパターン）と4-2や4-3の構成を組み合わせて解いた経験が執筆者にはほとんどないため，要チェックかもしれません．4-4についても，最近筆者が気づいた手法なので開拓の余地があると思います.
本構文を用いた解を見つけるときに，理由づけがしにくいものに関してはsolverに頼るのがbestと言わざるを得ません．
もちろん安直に作成しても良いですが，使用用途に応じて形ごとに分けたり，同じ形やほとんど意味のないものを省く仕組みを入れたり（＝枝刈り）することが非常に大事になります．
mapに対して解けるかどうか，ではなく数列のみを照合するプログラムを作成すると検索時間も短く，応用も効きやすくなります．
HOJの仕組み上，天井関数で数列が決まる点に注意です．
12B構文のA,B,C,Dの正負に応じてsolverを分けてしまうというのも手です．
特にBとDがマイナスとなるケースは，第二項の後ろに命令をつけるものも意味を持ちます．
また，Dは0でも意味のあるケースが存在する点に注意です．
a(X):[0]a(X-i)[1]a(X-j)[2] a(k)という形のものの検索について（Xの係数は簡単のため1としていますがそうでなくても良いです)，枝刈り方法を列挙します．
もっと良いものもあるかもしれません．全てを検索するのはどうしても遅くなるので，この辺のアイデアは執筆者も知りたいです．
執筆：Ktya
12B_new_app.png 99件
[詳細]
HOJ_12Bapp_16.png 89件
[詳細]
HOJ_12Bapp_15.png 101件
[詳細]
HOJ_12Bapp_14.png 96件
[詳細]
HOJ_12Bapp_13.png 90件
[詳細]
HOJ_12Bapp_12.png 91件
[詳細]
HOJ_12Bapp_11.png 97件
[詳細]
HOJ_12Bapp_10.png 95件
[詳細]
HOJ_12Bapp_09.png 98件
[詳細]
HOJ_12Bapp_08.png 94件
[詳細]
HOJ_12Bapp_07.png 92件
[詳細]
HOJ_12Bapp_05.png 91件
[詳細]
HOJ_12Bapp_06.png 99件
[詳細]
HOJ_12Bapp_04.png 90件
[詳細]
HOJ_12Bapp_03.png 93件
[詳細]
HOJ_12Bapp_02.png 103件
[詳細]
HOJ_12Bapp_01.png 97件
[詳細]
